
Żeby wyjaśnić co to jest rekurencja, musisz najpierw zrozumieć co to jest rekurencja :). W tym tekście w prostych słowach omawiamy zagadnienia: silnia, ciąg Fibonacciego, rekurencja a przepełnienie stosu.
Miło nam przedstawić nowy cykl felietonów, dotyczący informatyki w szkolnictwie średnim i zawodowym. Nasz poradnik ma w prosty i dość luźny sposób przedstawić zagadnienia zwiazane z informatyką i podstawami programowania. Zapraszamy do lektury!
Wszystko co trzeba wiedzieć o rekurencji
Czy zdarzyło się Wam chociaż raz w życiu przeżyć swoisty „dzień świstaka”? Kiedy to w ciągu dnia w pracy, w szkole (czy w jakimkolwiek innym miejscu) cały czas mieliście do czynienia z tym samym zadaniem lub sytuacją? Gdyby nasze życie było w tym momencie algorytmem, to można byłoby uznać, że wpadliśmy w „rekurencję”.
Co to jest rekurencja
Zacznijmy więc od samej definicji słowa rekurencja. Jak podaje „Encyklopedia algorytmów”, mówimy tutaj o odwołaniu się funkcji lub definicji do samej siebie, w celu uzyskania pętli. Mówiąc bardziej technicznie, podejście rekurencyjne polega na tym, że rozwiązanie problemu wyraża się za pomocą rozwiązania tego samego problemu dla mniejszych danych wejściowych. Choć sama metoda zastosowania rekurencji jest stosunkowo prosta, to jest obarczona pewnym ryzykiem – Skoro funkcja jest wywoływana „w kółko”, to w pewnym momencie może zacząć mocniej obciążać pamięć, a w skrajnych wypadkach doprowadzać do przepełnienia stosu. O tym, jak sobie z tym radzić oraz o metodach obliczania rekurencji dowiecie się z poniższego artykułu.
Wyznaczanie silni sposobem rekurencyjnym
Silnia
Zacznijmy od podstaw, jak w szkole podstawowej, czyli coś niecoś na temat silni. Choć w szkole nie zawsze nas o tym uczyli, że silnia może służyć do obliczeń rekurencyjnych, to jak najbardziej się do tego nadaje. Jak zapewne możecie kojarzyć, podstawowy wzór na silnie prezentuje się następująco:
n! = 1 ⋅ 2 ⋅ 3 ⋅...⋅ (n − 1) ⋅ n
Oznacza on, że silnia liczby n (n!, czyt. en silnia) to iloczyn kolejnych liczb naturalnych od 1, aż do n. Podstawiając dane do wzoru, możemy otrzymać następujące przykłady:
1! = 1
2! = 1 ⋅ 2 = 2
3! = 1 ⋅ 2 ⋅ 3 = 6
4! = 1 ⋅ 2 ⋅ 3 ⋅ 4 = 24
5! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 = 120
i tak dalej...
Patrząc na to możemy zobaczyć pewną zależność. Jeżeli chcielibyśmy policzyć wartość n! (np. 4!), to wcześniej powinniśmy policzyć (n-1)! (czyli 3!). Interpretując powyższą zależność i równania, dostajemy taki zapis: 4! = 3! ⋅ 4. W związku z tym można stworzyć następujący wzór:
n! = (n - 1)! ⋅ n
Może część z Was zauważyło co tu zaszło? Jeżeli chcemy wyliczyć silnie danej liczby, to wcześniej należy policzyć silnie liczby o jeden mniejszej. Właśnie w tym momencie pojawia się zjawisko rekurencji, które wyraża się następującym równaniem:

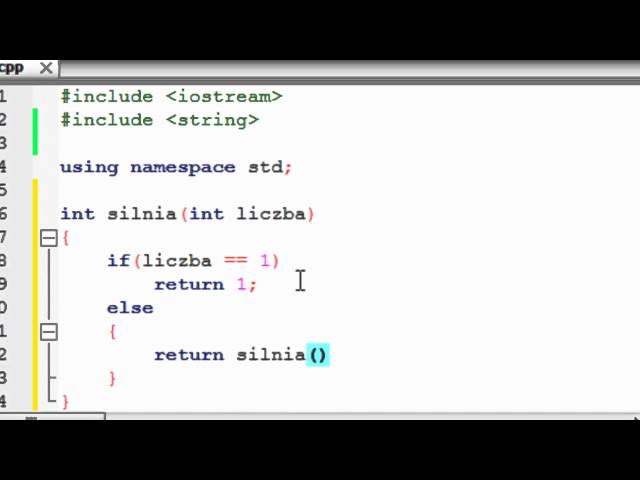
Silnia będzie liczona tak długo, dopóki jej wyliczenia będą większe od 1. Bardzo klarownie tłumaczy to poniższy film, w którym opisywany jest przykład w języku C++:
Ciąg Fibonacciego i jego "magiczne" właściwości
Innym, bardzo ciekawym przykładem rekurencji jest wzór Fibonacciego, zwany również spiralną filotaksją. Jest on o tyle ciekawy, że występuje w wielu elementach w naturze (liczba płatków kwiatów, warstwy szyszek, kwiat słonecznika, gałęzie drzew itd.) i jest ściśle powiązany ze złotym ciągiem czy złotym podziałem.
Otóż ciąg ten składa się z liczb naturalnych, rozpoczynających się od 0 i 1. Każda następna wartość jest sumą dwóch poprzednich. Wygląda to w ten sposób:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
i tak dalej...
Ciąg ten ma w sobie „ukrytą” zależność. Otóż jeżeli weźmiemy dowolny wynik z ciągu (np. 8) i podzielimy go przez poprzedni wynik (w tym przypadku 5), to wynik wyniesie około 1,6 (im wyższe wartości wybierzemy, tym iloraz będzie dokładniejszy). Wynik ten oznacza się grecką literą φ (Phi, czyt. fi) i to on właśnie wyznacza wspomniany wcześniej „złoty podział”, bądź jest nazywany „boską proporcją”.
Jeżeli chodzi natomiast o samo równanie rekurencyjne, to prezentuje się one następująco:

Zastosowanie tego ciągu w programowaniu bardzo profesjonalnie przedstawia Mirosław Zelent na swoim materiale:
Rekurencja a przepełnienie stosu
Przepełnienie stosu, czyli "stack overflow"
Jak wspominałem na początku tego felietonu, funkcje rekurencyjne mogą utrudnić życie początkującym programistom. Otóż programując aplikacje, tak naprawdę tworzymy dla komputera listę „rozkazów” do wypełnienia. Generalnie funkcja dysponuje określonym obszarem pamięci, gdzie trzyma swoje zmienne lokalne. Gdy w jej ramach odpalamy nową funkcję, to stan naszych zmiennych jest zapisywany i cała funkcja jest odkładana na stosie wywołań. W momencie zakończenia obliczeń dana funkcja jest zdejmowana ze stosu i jej wartości są oznaczane jako nieużywane, a obliczona wartość jest przekazywana do funkcji wywołującej.
W przypadku rekurencji ta sama funkcja będzie znajdować się na stosie wiele razy, aż do osiągnięcia wartości definiującej określony próg akceptacji w którym stwierdzamy, że możemy zwrócić wartość zamiast tworzyć nowe wywołania funkcji. Jeżeli natomiast źle zaimplementujemy warunek akceptacji to może się zdarzyć, że funkcja będzie wykonywana nieograniczona ilość razy, dokładając coraz to nowsze wywołania do stosu wywołań i powodując jego przepełnienie.
W celu rozwiązania tego problemu, warto zastosować chociażby taką metodę, jak rekurencję ogonową. W dużym uproszczeniu chodzi o to, aby wywołać funkcję na końcu aktualnej funkcji. Rekurencja ogonowa jest w zasadzie wtedy, gdy istnieje tylko jedno wywołanie rekurencyjne i to wywołanie jest ostatnią instrukcją w funkcji. Prostą funkcję rekurencyjną ogonową można przedstawić chociażby w ten sposób:
unsigned int f( unsigned int a )
{
if ( a == 0 ) {
return a;
}
return f( a - 1 ); // tail recursion
}
Mam nadzieję, że udało mi się przybliżyć temat rekurencji w możliwie klarowny sposób. Dajcie znać, jak podoba się Wam pierwszy artykuł z tej serii – Czekam na Wasze opinie i komentarze.













Komentarze
2